При любом использовании данного материала ссылка на первоисточник обязательна!

материал позволяет предвидеть возможные будущие достижения в сумме двоеборья у атлетов различных весовых категорий в зависимости от возраста, в котором начаты занятия, а также определить перспективность атлета.

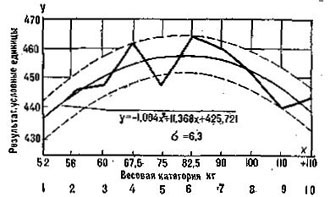
Важными показателями в подготовке тяжелоатлета являются ростовые данные. В связи с исключением из программы соревнований жима рост атлетов несколько изменился. По нашим данным (показатели 131 тяжелоатлета), у выступающих _в настоящее время тяжелоатлетов рост по весовым категориям составил: в

весовой категории 52 кг в среднем 153,8 см, 56 кг — 155,7, 60 кг — 157,7, 67,5 кг — 161,3, 75 кг — 164,9, 82,5 кг — 168,6, 90 кг — 172, 100 кг — 177, 110 кг — 181,9, 120 кг — 186,8, 130 кг — 191,6 (коэффициент корреляции веса и роста составил 0,891).

Нужно заметить, что ростовые данные в каждой из весовых категорий (за исключением 90 кг) в среднем увеличились. Меньше это увеличение в весовых категориях 67,5 — 82,5 кг и больше в крайних весовых категориях — 52 — 60 кг и 100 кг и выше.

СТАТИСТИЧЕСКИЙ АНАЛИЗ И ПРОГНОЗИРОВАНИЕ ДИНАМИКИ ВЫСШИХ ДОСТИЖЕНИЙ ТЯЖЕЛОАТЛЕТОВ

При отборе и подготовке спортсменов на различных уровнях управления, планирования, прогнозирования, учета, отчетности и в научно-прикладных исследованиях в спорте важная роль отводится анализу результатов за периоды определенной продолжительности. Особое место занимают данные о динамике мировых достижений, являющиеся ориентиром для определения, оценки и прогноза конкретных спортивных показателей спортсменов (М. В. Стародубцев, А. С. Медведев, 1979; Л. С. Хоменков, 1980; Г. П. Семенов, 1983, и др.).

Анализ мировых достижений в тяжелой атлетике с целью их прогнозирования на последующий период был предметом исследований в работах ряда специалистов. При этом в качестве мировых достижений рассматривались: олимпийские достижения в троеборье (Ю. Лукашин, 1965), мировые рекорды в сумме троеборья (А. С. Медведев, Р. А. Роман, А. В. Черняк, 1966), достижения шести лучших тяжелоатлетов мира в отдельных упражнениях и сумме троеборья (А. В. Черняк, 1970), результаты в сумме двоеборья десяти лучших тяжелоатлетов года независимо от весовых категорий (Ю. А. Сандалов, М. В. Стародубцев, П. А. Полетаев, В. В. Тамарлаков, 1982), мировые рекорды в упражнениях и сумме двоеборья (Н. П. Лапутин, В. Г. Олешко, 1982).

При прогнозировании результатов все исследователи пользуются методом экстраполяции моментных или интервальных данных, полученных по состоянию на определенные моменты времени или за тот или иной период (как правило, лучшие результаты за год). Поскольку же всякая экстраполяция является лишь приблизительным определением каких-либо значений, находящихся вне ряда известных значений (С. В. Начинская, 1978), т. е.

продлением линии, отражающей тенденцию прошлых наблюдений (данных), закономерно возникает вопрос об определении степени вероятности такого прогноза, а также доверительных интервалов прогнозируемых результатов.

К сожалению, в опубликованных работах мы не обнаружили величин вероятности даваемых прогнозов и доверительных интервалов прогнозируемых результатов. Известные нам работы с анализом и прогнозом мировых достижений в тяжелой атлетике страдают, на наш взгляд, недостаточно высоким уровнем обобщений и в особенности тем, что в этих исследовательских попытках не были использованы методы восхождения от абстрактного к конкретному и от общего к частному, являющиеся, как известно, методологической основой изучения всех сложных явлений и процессов.

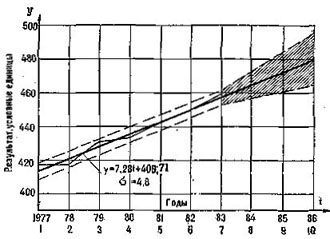
В связи с наличием различных весовых категорий в тяжелой атлетике исследователи были вынуждены анализировать достижения, показанные в них, раздельно *. Разработка методики выражения результатов тяжелоатлетов различных весовых категорий в сопоставимых оценках (М. В. Стародубцев, 1962 — 1982) позволяет выявить общую тенденцию динамики спортивных достижений тяжелоатлетов и, исходя из нее, дать прогноз конкретных достижений тяжелоатлетов в отдельных весовых категориях.

С учетом сказанного мы поставили задачу изучить динамику высших мировых достижений (рекордов) тяжелоатлетов за период с

* Исключение в этом плане представляет работа А. В. Черняка («Теория и практика физической культуры», 1970, № 8), в которой результаты в килограммах переводятся в условные единицы с помощью формулы.

1947 по 1983 г.* и на этой основе дать прогноз результатов в сумме двоеборья с обоснованными доверительными интервалами их значений на последующий, трехгодичный, период.

Исследование динамики явления, т. е. его развития во времени, проводится с помощью построения и анализа особых рядов, представляющих числовую последовательность наблюдений во времени. Они называются рядами развития или динамическими (временными) рядами. В них в одной строке (столбце) указываются последовательные периоды времени, в другой — фактически соответствующие этим периодам наблюдения, которые называются уровнями временного ряда.

Основным правилом построения временных рядов является следующее: уровни ряда должны состоять из однородных, сопоставимых величин. Поэтому перед построением таких рядов мы условились:

1. До 1973 г. (до начала регистрации мировых рекордов в сумме двоеборья) в качестве высших достижений считать сумму мировых рекордов в рывке и толчке, округленных с недостатком до числа, кратного 2,5. Например, в 1965 г. у легковесов (67,5 кг) рекорды мира в рывке и толчке равнялись соответственно 134 и 168,5 кг. Для них, согласно нашему условию, высшими достижениями в сумме двоеборья следует считать 300 (132,5+167,5) кг. В последующий период (с 1973 г.) эти условные суммы заменяются превышающими их официальными мировыми, рекордами в сумме двоеборья.

2. Для получения сравнимых данных результаты в килограммах оценивать по таблице сопоставимых оценок (М. В. Стародубцев, 1981)** в условных единицах (усл. ед.). При этом для самой тяжелой весовой категории во все годы использовали шкалу св. 110 кг. Полученные производные динамические ряды мировых достижений в каждой весовой категории, средние значения усл. ед. и коэффициенты их вариации представлены в табл. 1.

Как видно из этой таблицы, мировые достижения во всех весовых категориях росли неравномерно. Нередко они не обновлялись по нескольку лет. Это происходило, как правило, в тех случаях, когда значения усл. ед. мировых рекордов в одной или ряде весовых категорий значительно превышали средние значения по всем весовым категориям, характерные для данного года. Можно сказать, что спортсмены, устанавливающие такие рекорды, как бы обгоняют время (Ю. А. Сандалов), т. е. забегают вперед относительно общего уровня развития высших достижений. Что же касается средних значений усл. ед. мировых достижений в весовых категориях, то они повышались, как пра-

* Мировые рекорды 1983 г. учтены по состоянию на 1 декабря.

** См. «Советский спорт», 24 июля 1981 г.

вило, непрерывно. Только в год введения новых весовых категорий отмечалось отклонение от этой закономерности — понижение среднего уровня рекордов. Так было в 1951 г. с введением весовых категорий 90 и свыше 90 кг и в 1969 г. с введением весовых категорий 52, 110 и свыше 110 кг. Введение весовой категории 100 кг в 1977 г. также значительно уменьшило средний годовой прирост усл. ед. мировых достижений.

Разброс же средних значений усл. ед. мировых достижений, напротив, постепенно уменьшался. Коэффициент вариации с 8,2% в 1947 г. снизился до 1,8% в 1983 г., что отражает тенденцию к нивелированию уровней достижений тяжелоатлетов разных весовых категорий.

Небезынтересно отметить и такой факт. В 1947 г. только в легкой весовой категории мировое достижение в сумме двоеборья было на 2,5 кг больше нормы мастера спорта СССР по классификации 1981 — 1984 гг., а в тяжелом весе (в то время свыше 82,5 кг) оно равнялось норме нынешнего I спортивного разряда. Так, рост спортивных достижений влечет за собой изменение представления о спортивных нормах.

В табл. 2 представлены обобщенные характеристики исследуемых временных рядов: нормированный относительный и средний абсолютный приросты (усл. ед.) мировых достижений.

Нормированный прирост по своей сути является критерием оценки эффективности определенного цикла подготовки тяжелоатлетов различных весовых категорий (В. А. Масленников, С. Г. Филановский, 1975; М. В. Стародубцев, 1982)*. Он определялся относительно достижения 400 кг (464 усл. ед.) в весовой категории 82,5 кг по формуле:

E_дв = 0,000464r₂ (r₂, — r₁).

Здесь E_дв — нормированный прирост суммы двоеборья, r₂ — оценка высшего достижения в конце рассматриваемого периода, усл. ед. r₁ — оценка достижения в начале периода, усл. ед. При анализе данных по этому показателю мы выделили шесть периодов. Периоды 1947 — 1968 и 1969 — 1982 гг. выделены в связи с введением в 1969 г. новых весовых категорий — 52, 110 и свыше 110 кг. Далее анализируются три периода равной продолжительности (с 1970 по 1982 г.) и полный динамический ряд — с 1947 по 1983 г.

Как видно из табл. 2, нормированный прирост высших достижений в сумме двоеборья в 1947 — 1968 гг. был наибольшим в крайних — самой легкой и самой тяжелой — весовых категориях, наименьший — в категории 82,5 кг, а коэффициент вариации прироста в этот период составил 29,6%. Согласно градациям спортивной метрологии, это очень большая изменчи-

* См. «Теор. и практ. физич. культ.», 1975, № 5, с. 20-21; 1982, № 12, с. 47.

Таблица 1

Временные ряды мировых достижений тяжелоатлетов в сумме двоеборья в сопоставимых оценках (усл. ед.)

вость. В 1969 — 1982 гг. картина изменилась: в группу лидеров по нормированному приросту достижений вошли категории 110, 82,5 и 90 кг, а категория 56 кг стала в этом смысле отстающей.

На наш взгляд, причиной столь резкого снижения нормированного прироста высших достижений в этом весе явилось введение в 1969 г. новой весовой категории — 52 кг, в которую перешли многие перспективные атлеты из категории 56 кг.

Судя по коэффициентам вариации, изменчи-

вость нормированных приростов суммы двоеборья в весовых категориях была очень высокой в обоих периодах. Средние же значения их оказались практически одинаковыми, хотя продолжительность первого периода составляет 21 год, а второго — 13 лет.

Скачкообразный характер изменения анализируемых нормированных приростов наглядно показывают их средние значения по периодам времени одинаковой продолжительности.

По данным табл. 2 нетрудно установить, что средние нормированные приросты в 1970 —

Таблица 2

Нормированный и средний приросты мировых достижений тяжелоатлетов в сумме двоеборья

1974 и 1974 — 1978 гг. несущественно различаются между собой (р > 0,05). А в 1978 — 1982 гг. отмечено достоверное увеличение этого параметра по сравнению с предыдущими (р = 0,05). Сходная картина наблюдалась и ранее. В частности, для периодов 1950 — 1954, 1954 — 1958, 1960 — 1964 и 964 — 1968 гг. средние значения нормированных приростов составляют соответственно 1,2, 2, 4,6 и 2,7%, в чем можно убедиться на основании данных табл. 1. Это незатухающее скачкообразное повышение эффективности подготовки тяжелоатлетов можно объяснить улучшением условий материальной жизни общества, прогрессом спортивной науки, совершенствованием отбора перспективных тяжелоатлетов, методики и организации их подготовки, эффективности тренировочных (нагрузочных) и восстановительных средств и другими факторами.

За период 1947 — 1982 гг. наибольший нормированный прирост рекордных достижений оказался в самой тяжелой весовой категории. Первенство за этой категорией останется и при E_дв = 33,9%, т. е. в том случае, если для оценки результата 1947 г. (310 кг) использовать таблицу сопоставимых оценок для категории 110 кг. Среднее значение нормированного прироста по всем весовым категориям в рассматриваемый период составило 31%, а коэффициент вариации оказался на отметке 12,9%, что в спортивной метрологии считается средним рассеиванием. При этом более эффективным процесс роста достижений был в весовых категориях 82,5 кг и выше.

Приведенные данные позволяют говорить о том, что различие весовых категорий тяжелоатлетов мало сказывается на эффективности рос-

та их высших достижений, хотя некоторое преимущество в этом отношении имеют спортсмены более тяжелых весовых категорий.

Итак, проведенный анализ позволил выявить ряд закономерностей (тенденций) динамики мировых рекордов. Естественно предположить, что эти тенденции будут действовать и в ближайшем будущем, т. е. должны учитываться при прогнозировании.

Важнейшей задачей анализа временных рядов является определение основной закономерности (общей тенденции) изменения изучаемых явлений во времени (Г. С. Кильдишев, А. А. Френкель, 1973). На основании полученных данных исследуемой динамики ее основную тенденцию можно сформулировать как скачкообразно протекающий прогресс мировых достижений тяжелоатлетов. Для того чтобы далее выразить эту общую тенденцию изменения мировых рекордов в функциональной зависимости, следует произвести сглаживание (аналитическое выравнивание) исследуемого временного ряда. Это одно из предварительных условий решения задачи прогнозирования.

Вторым условием является определение наиболее информативного периода фактической динамики мировых рекордов для последующего их прогнозирования. Наиболее важным и информативным периодом будет, безусловно, конечный период развития, за точку отсчета которого целесообразно взять 1977 г., когда с введением весовой категории 100 кг завершилось формирование ряда весовых категорий в тяжелой атлетике. Для этого же периода, как было отмечено, судя по нормированному приросту, характерен и новый скачок эффективности роста достижений.

Рис. 1. Выравненные по прямой усредненные оценки (усл. ед.) мировых рекордов в сумме двоеборья за период с 1977 по 1983 г. и прогноз на 1984 — 1986 гг.
Нижний ряд цифр — порядковые номера уровней динамического ряда (годы) в данном периоде (значения t)

Рис. 2. Выравненные по параболе оценки (усл. ед.) мировых рекордов в сумме двоеборья 1982 г. в разных весовых категориях
Нижний ряд цифр — порядковые номера весовых категорий (значения X)

При выборе вида функции времени f(t),t.e. линии, которую называют трендом, при аналитическом выравнивании динамического ряда принимают во внимание характер (скорость) изменения уровней ряда, т. е. возникает необходимость в определении среднего прироста. Он вычисляется по формуле:

Y_n – Y₁
Y= —————— ,
n – 1

где Y — средний абсолютный прирост, Y_n — конечный в рассматриваемом периоде уровень ряда, Y₁ — первый (исходный) в рассматриваемом периоде уровень ряда.

В табл. 2 приведены 3-летние среднегодовые приросты усл. ед. мировых рекордов за пери-

од с 1977 по 1983 г., разбитый на три этапа, и усредненные значения среднегодовых приростов. Сравнивая последние между собой, мы видим, что они достаточно близки друг другу. Следовательно, для выравнивания ряда сопоставимых оценок мировых рекордов за указанный период можно взять прямую линию. Заметим, что, согласно статистическим руководствам, при экстраполяции по линейному тренду должно быть не менее шести наблюдений.

На рис. 1 изображены фактические средние значения, полученные из усл. ед. мировых рекордов (ломаная линия), и выравненные значения (сплошная прямая линия). Выравнивание произведено при помощи чисел Чебышева (А. К. Митропольский, 1961). На этом же рисунке показана зона колебаний, ограниченная пунктирными прямыми, проведенными по обе стороны от сплошной прямой, на расстоянии, равном стандартной ошибке уравнения прямой.

Согласно рис. 1, фактические оценки ни разу не вышли из зоны колебаний. Поэтому полученное уравнение может быть с достаточным основанием использовано для прогнозирования оценок на 1984 — 1986 гг. методом экстраполяции.. На рис. 1 зона экстраполяции заштрихована.

По уравнению прямой мы определили вероятные средние оценки (усл. ед.) мировых рекордов в сумме двоеборья на 1984 — 1986 гг. (соответственно 465; 472,3 и 479,5 усл. ед.). Затем фактические оценки усл. ед. в отдельных весовых категориях выравнили в каждом году периода с 1974 по 1983 г. (на рис. 2 показан пример выравнивания) и вычислили отношения выравненных значений оценок (усл. ед.) к среднему значению данного года. Усредненные в каждой весовой категории за весь период эти отношения оказались равными (в порядке весовых категорий): 0,986; 0,997; 1,002; 1,004;. 1,005; 1,008; 1,006; 1,004; 0,995 и 0,990. Последние мы использовали в качестве поправочных коэффициентов при вычислении точечных (выраженных одним числом) прогнозов оценок мировых рекордов (усл. ед.) в каждой весовой категории, представленных в табл. 3.

Известно, что точное совпадение фактических данных и точечных прогнозов — явление маловероятное. Поэтому возникает необходимость в доверительных интервалах прогноза. Для линейного тренда этот интервал определяется (Е. М. Четыркин, 1977) как:

           _^                         
y_t+L ± S_yK*,

где y_t+L — точечный прогноз для данного периода упреждения; S_y — среднее квадратическое отклонение фактических наблюдений от расчетных значений у; К* — величина, зависящая от числа наблюдений (длины ряда динамики), длительности периода, для которого делается экстраполяция, и t — статического

критерия Стьюдента (значения К* указываются в специальных таблицах). Так, при экстраполяции ряда динамики, изображенного на рис. 1, значения К* при уровне вероятности 0,9 будут соответственно равны 2,638; 2,875; 3,140, а поправки к точечным прогнозам — произведениям этих коэффициентов на величину стандартной ошибки уравнения тренда, т. е. на 4,8. В качестве примера найдем доверительный интервал прогноза на 1985 г. в категории 75 кг. Имеем:

475 ± 4,8 ∙ 2,875, т. е. 461 — 489 усл. ед.

Следовательно, с вероятностью 0,9 можно утверждать, что у полусредневесов мировой рекорд в сумме двоеборья в 1985 г. будет не менее 372,5 кг и не более 390 кг.

Аналогичным образом мы рассчитали доверительные интервалы мировых рекордов в сумме двоеборья для всех весовых категорий.

Таблица 3

Прогноз мировых рекордов тяжелоатлетов в сумме двоеборья

Данные табл. 3 могут быть использованы при разработке разрядных норм по тяжелой атлетике на 1985 — 1988 гг. и модельных характеристик для отбора кандидатов в сборную команду страны.

В заключение отметим, что в основу полученного нами прогноза мировых достижений положено аналитическое выражение функции времени. При этом время рассматривается как независимая переменная, а уровни ряда (мировые рекорды в сумме двоеборья) — как функция этой независимой переменной. Естественно, время определяет рост спортивных достижений только потому, что оно несет в себе определен-

ное содержание — соответствующую подготовку тяжелоатлетов к новым рекордам. Ясно, что без такой подготовки, включающей многочисленные факторы, влияющие на развитие высших достижений тяжелоатлетов, а также без наличия самих талантливых тяжелоатлетов, способных к установлению рекордов, время само по себе не обеспечит дальнейшего их роста. Поэтому кроме отмеченных в данной статье статистических закономерностей (тенденций) развития мировых рекордов в прогнозе нужно учитывать и эти реальные предпосылки (факторы).

К ВОПРОСУ ПРОГРАММИРОВАНИЯ ТРЕНИРОВОЧНОЙ НАГРУЗКИ ТЯЖЕЛОАТЛЕТОВ

Эффективность процесса управления во многом зависит от методов, позволяющих получать информацию об изменениях в состоянии спортсменов и в техническом мастерстве, вы-

званных выполнением запланированной двигательной нагрузки, т. е. от системы обратной связи в целях коррекции программы.

В тяжелой атлетике крайне мало исследова-