При любом использовании данного материала ссылка на первоисточник обязательна!
грамма: отдельные дистанции, командные гонки).
13. Классификационные соревнования в группах (программа: отдельные дистанции, многоборье).
14. Первенство школы по эстафетам (II тур).
15. Матчевая встреча двух-трех спортивных школ (программа: отдельные дистанции, многоборье) .
16. Первенство города среди спортивных школ (программа: отдельные дистанции, многоборье, эстафеты).
17. Классификационные соревнования внутри групп (программа: отдельные дистанции).
18. Городские соревнования на приз героя, ветерана конькобежного спорта и т. п.)
19. Первенство школы по стайерскому бегу, III тур (программа: отдельные дистанции, групповые забеги).
Февраль
20. Первенство области (республики, ЦС ДСО и ведомств).
21. Соревнования школы на приз шефов или приз катка (программа: отдельные дистанции, многоборье, эстафеты).
22. Контрольные соревнования внутри групп (программа: отдельные дистанции).
23. Первенство школы по командным гон-
кам, IV тур (программа: командные гонки).
24. Участие сильнейших конькобежцев в матчевой встрече двух-трех спортивных школ (программа: многоборье, эстафеты, командные гонки).
25. Классификационные соревнования — открытые старты школы (программа: отдельные дистанции — по выбору).
26. Республиканские и всесоюзные соревнования.
27. Классификационные соревнования внутри групп (программа: отдельные дистанции).
Март
28. Первенство спортивной школы по многоборьям (V тур).
29. Классификационные соревнования школы по спортивным разрядам (программа: отдельные дистанции).
30. Матчевая встреча сильнейших конькобежцев двух-трех школ (программа: отдельные дистанции, эстафеты, групповые и командные гонки).
31. Приз закрытия зимнего спортивного сезона (программа: отдельные дистанции, многоборье).
32. Классификационные групповые соревнования (программа: отдельные дистанции).
33. Всесоюзные соревнования.
НАУКА — ПРАКТИКЕ
МЕХАНОМАТЕМАТИЧЕСКОЕ ОБОСНОВАНИЕ ОБЕСПЕЧЕНИЯ БЕГА НА КОНЬКАХ СО СКОРОСТЬЮ 15 М/С
А. М. Дрыганов, Г. А. Титов, В. А. Горячев, ВНИИФК
На современном уровне развития конькобежного спорта возникает ряд проблем, связанных с обеспечением достижения высоких спортивных результатов. К одной из них относится проблема скоростно-силовой подготовленности конькобежца экстракласса для обеспечения скорости бега 15 м/с.
Эмпирические наблюдения за высококвалифицированными конькобежцами дают возможность оценить уровень развития физических качеств — силы и быстроты как фотографию сегодняшнего дня. Такие исследования только путем экстраполяции показывают дальнейшую дорогу к совершенствованию.
Есть и другой путь решения вопроса, который позволяет заглянуть в завтрашний день на основе механоматематического моделирования
предполагаемого движения. В частности, в ближайшем будущем скорости бега на коньках вплотную подойдут к рубежу 15 м/с, что обеспечит рекордные результаты в беге на 500 и 1000 м.
В настоящей работе на основании анализа общих закономерностей бега скорохода рассматривается механоматематическая модель с позиций его силового обеспечения. В качестве оценки силовой подготовленности предлагается определение скорости выпрямления ног при отягощении в 2,5 веса тела спортсмена.
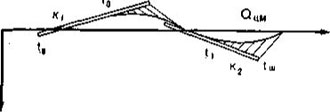
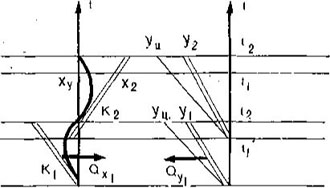
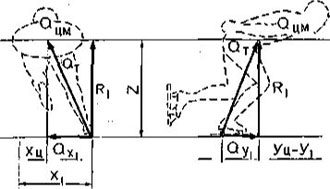
I. Общие закономерности динамики скоростного бега на коньках. Основной задачей конькобежца в соревновании является прохождение дистанции за минимальное время или, что то же самое, с максимальной скоростью V. Во
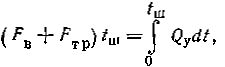 (I.3)
(I.3)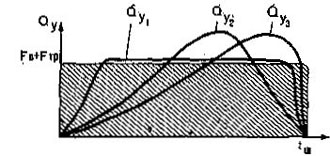
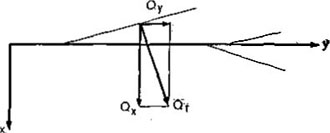
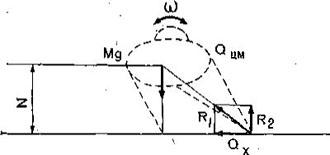
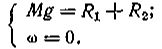 (I.4)
(I.4)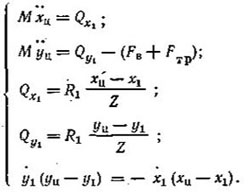 (II.1)
(II.1)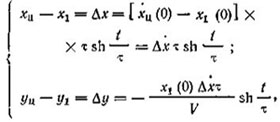 (II.2)
(II.2)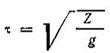 .
.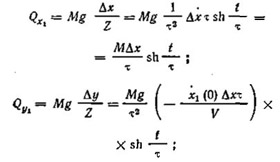 (II.3)
(II.3)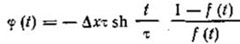 (II.5)
(II.5)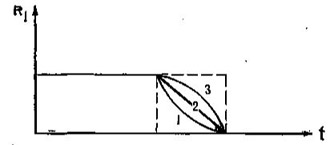
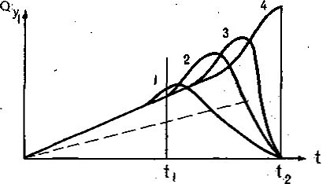
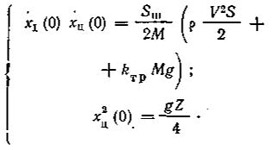 (II.6)
(II.6)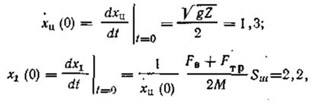
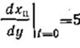 — угол наклона траектории ОЦМ к
— угол наклона траектории ОЦМ к 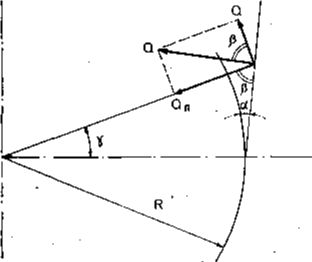
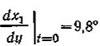 — угол наклона следа конька;
— угол наклона следа конька;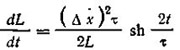 (II.7)
(II.7) (III.1)
(III.1)
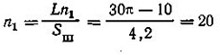 шагов;
шагов;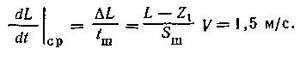
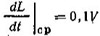 .
.