При любом использовании данного материала ссылка на первоисточник обязательна!
ветственно 76, 75 и 30°, у спортсменов II разряда — 55, 44 и 30°.
Сопоставляя технику бега конькобежцев II и III разрядов необходимо отметить, что в характеристиках движений испытуемых установлено только пять достоверных различий (22,7%). У спортсменов III разряда показатели времени I и II фаз на 16,0% больше, чем у спортсменов II разряда. Темп передвижения у них на 11,2%, а давление на пятку в фазе одноопорного отталкивания в начале и середине соответственно на 38 и 35,4% меньше, чем у спортсменов II разряда.
Анализируя динамограммы у спортсменов разных разрядов, можно отметить некоторые особенности в характере проявления усилий. Характер динамограмм у спортсменов I и II разрядов почти одинаков. У перворазрядников распределение усилий на носок в фазах отталкивания отличается плавным нарастанием силы, которая достигает максимального значения к концу II и началу III фазы. В фазе свободного скольжения давление на носок у спортсменов II разряда достоверно меньше. Отличие в распределении усилий на пятку заключается в большем давлении к середине II и к началу III фазы. У спортсменов II разряда наблюдается более позднее нарастание максимального усилия и неравномерное распределение усилия в I фазе, что связано с неумением полностью переносить вес тела на опору.
Динамограмма конькобежцев III разряда также имеет свои отличия по характеру распределения усилий. Спортсмены III разряда распределяют усилия на носок и пятку до середины II фазы равномерно. Затем, начиная с середины II фазы, давление на пятку, так и не увеличившись, снижается, а давление на носок к началу III фазы незначительно увеличивается (до 66 кг). Таким образом, спортсмены
III разряда нерационально выполняют ведущий элемент движения — отталкивание. Как правило, у них нет активного смещения туловища в сторону, оно заменено у них «шаганием вперед», как в ходьбе и в беге. Причина нерациональных движений кроется, на наш взгляд, в слабом уровне подготовленности отдельных групп мышц.
На основании вышеизложенного можно сделать следующие выводы:
1. Техника движений при беге на коньках у спортсменов разной квалификации имеет существенные различия. Количество достоверных различий увеличивается у спортсменов, значительно отстоящих друг от друга по своей квалификации.
2. Техника спортсменов, близких по своему уровню подготовленности, отличается в меньшей степени. Так, спортсмены II и III разряда по техническому уровню отличаются незначительно. Различия составляют 22,1%. Спортсмены I и II разрядов имеют 41% достоверных различий, а I и III разрядов — 72%.
3. Наиболее существенные различия между спортсменами разных разрядов наблюдаются по следующим характеристикам скользящего шага: в величине давления на пятку и носок в фазах, во времени фаз скользящего шага, в длине пройденного пути за 1 фазу и скользящий шаг, в темпе передвижения и амплитуде разгибания в суставах. Выявленные особенности в структуре движении конькобежцев разного уровня подготовленности позволят сосредоточить внимание на устранении отдельных недостатков в технике, рационализации и оптимизации распределения усилий в скользящем шаге и разработке преемственной методики технического совершенствования на различных этапах становления технического мастерства конькобежцев.
В. А. Балакин, Е. А. Духовской, В. Г. Шадрин, Москва
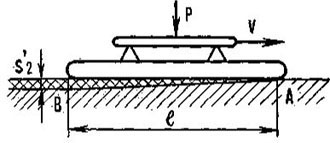
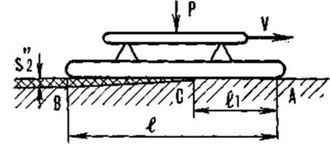
Вопрос взаимодействия конька со льдом с объяснением физической природы явления «скользкости льда» рассматривается в ряде работ, например в работах известного советского ученого В. Д. Кузнецова (1947), английского физика Ф. П. Боудена (1968) и т. д.
Сам термин «скользкость льда» указывает на то, что в области контакта конек — лед очень небольшой коэффициент трения. Количественные значения коэффициентов трения (f
![]() 0,02 — 0,04) соответствуют условиям контакта твердых тел, разделенных жидкостью, или так называемому гидродинамическому тре-
0,02 — 0,04) соответствуют условиям контакта твердых тел, разделенных жидкостью, или так называемому гидродинамическому тре-
нию. Таким образом, скользкость льда объясняется наличием тонкой пленки воды, образующейся на границе контакта конек — лед и выполняющей роль смазки.
Однако в имеющейся научно-технической и спортивной литературе, посвященной вопросу взаимодействия конька со льдом, отсутствует какая-либо теория, позволяющая проводить количественный анализ физических процессов, происходящих на границе контакта конек — лед.
Рассмотрим задачу об оплавлении тонкого Поверхностного слоя льда под коньком.
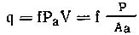 ,
(1)
,
(1)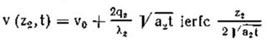 ,
(2)
,
(2)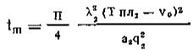 ,
(3)
,
(3)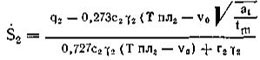 , (4)
, (4)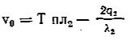 .
(6)
.
(6)