При любом использовании данного материала ссылка на первоисточник обязательна!

ских систем правой и левой ноги. Номинальная мощность конькобежца, равная 0,5 л. с, при рациональном ее использовании достаточна, чтобы иметь рекордные результаты на соревнованиях. В этом вопросе ему поможет теория — динамика конькобежца.

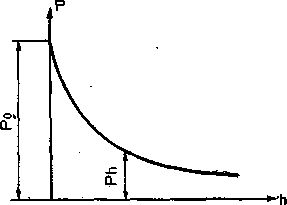
В результате теоретического анализа динамических качеств конькобежца выявлена возможность повышения номинальной скорости за счет некоторого уменьшения коэффициента трения скольжения и снижения силы давления полоза конька Q на лед. Первое возможно за счет полировки полоза конька, за счет мягкой постановки конька на лед, бесшумного скольжения, так как малейшее срезание льда полозом ведет к нерациональному расходованию мощности конькобежца. Второе возможно за

счет рациональной работы конькобежца в фазах скользящего шага.

Для получения необходимых данных при решении уравнений тягового баланса конькобежцу необходимо уточнить некоторые параметры:

1)   коэффициент , точное значение которого можно получить только путем экспериментальных исследований и испытаний на конькобежцах для различных условий движения;

2)   силу давления полоза конька Q на лед, полученную также путем эксперимента;

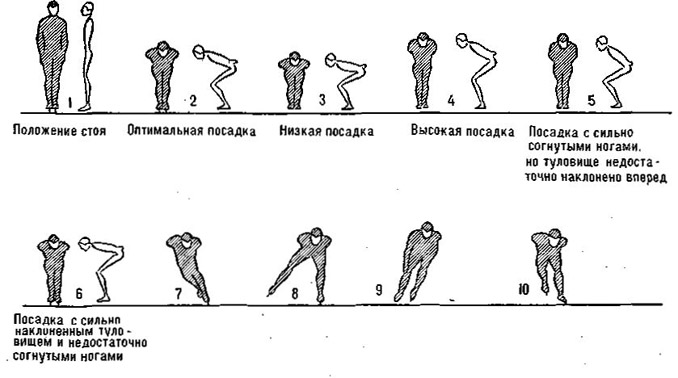
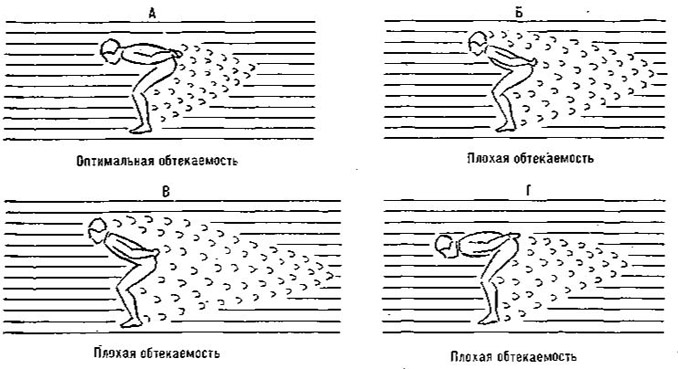
3)   коэффициент обтекаемости к. Точное значение данного коэффициента может быть определено только с помощью аэродинамической трубы (для низкой, средней и высокой посадки, при различном положении рук).

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ТЕХНИКИ СКОРОСТНОГО БЕГА НА КОНЬКАХ

Совокупность двигательных действий, осуществляемых с целью достижения определенной скорости бега, называется техникой скоростного бега на коньках, а педагогический процесс, направленный на овладение техникой и постоянное ее совершенствование, — технической подготовкой. Основная цель процесса совершенствования технического мастерства конькобежцев — это выработка наиболее эффективных для каждого конкретного случая способов локомоции. При этом техническая подготовка осуществляется в единстве с физической, которая предусматривает развитие силы, быстроты, выносливости, гибкости и ловкости. Принцип тесной взаимосвязи всех сторон подготовки конькобежцев в значительной степени определяет необходимость постоянного совершенствования структуры двигательных действий в соответствии с повышающимся уровнем физических качеств.

Конькобежец с точки зрения физики является материальным телом, и движение, наблюдаемое нами при беге, есть механическое движение, под которым понимают изменение взаимного положения материальных тел и отдельных их точек относительно друг друга. Поэтому механизм движений конькобежца в основном подчиняется законам механики в их специфическом преломлении для биологических систем. Тренер и спортсмен должны знать и общие законы механики, и тот внутренний механизм, посредством которого осуществляется реализация этих общих законов в каждый конкретный момент движений конькобежца. Но прежде чем приступить к анализу техники скоростного бега на коньках, необходимо рассмотреть и сис-

тематизировать различные законы физики, данные анатомии и физиологии человека. Это позволит глубже понять основные закономерности и целесообразность той или иной структуры движений, а также создаст подлинно научную основу совершенствования технического мастерства конькобежцев.

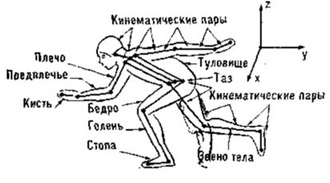
I. Динамическая анатомия (кинезиология) конькобежца. Благодаря сокращению мышц возникает сила, которая приводит в действие систему рычагов, созданных костями конькобежца. В беге на коньках основная нагрузка приходится на ноги. Туловище и голова практически не участвуют непосредственно в осуществлении движения и создании движущих сил. Однако от их исходного положения и взаимодействия с ногами и руками в существенной мере может зависеть общая эффективность двигательных действии. Таким образом, при анализе и описании техники скоростного бега на коньках для каждого момента движении обязательно необходимо указывать и рассматривать положение всех основных частей тела.

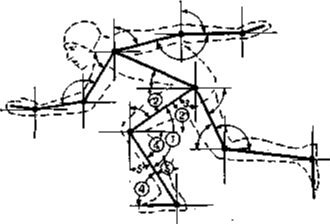
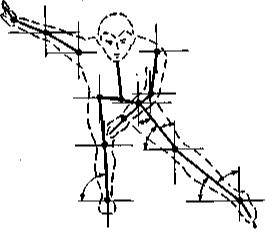
Части тела конькобежца, имеющие подвижные соединения, называются звеньями. Все звенья соединяются между собой с помощью суставов. Подвижное соединение двух звеньев составляет кинематическую пару, а последовательно или разветвленное соединение нескольких кинематических пар составляет кинематическую цепь. Кинематические цепи могут быть незамкнутыми (в каждом соединении возможны изолированные движения), замкнутыми и замкнувшимися (движение одних звеньев вызывает движение других). При анализе техники бега необходимо указывать положение

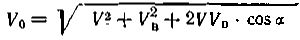
Рис. 1

следующих звеньев тела: кисти, предплечья, плеча, туловища, головы, бедра, голени и стопы. В большинстве случаев кисть руки и стопу мы будем рассматривать как единые целые звенья, хотя они и состоят из значительного числа самостоятельных звеньев. Такое допущение целесообразно и возможно, поскольку, например, звенья стопы находятся в ботинке в фиксированном состоянии и представляют собой как бы единое целое. В отдельных случаях при анализе техники бега необходимо указывать положение таза. На рис. 1 указаны основные звенья, части тела конькобежца, кинематические пары и кинематические цепи, расположение которых в пространстве и относительно друг друга постоянно меняется в процессе бега.

Любое свободное тело имеет шесть степеней свободы движения: три поступательного вдоль трех осей в системе прямоугольных координат X, У, Z (вверх-вниз, вперед-назад, вправо-влево) и три вращательного вокруг соответствующих осей. В принципе человек как единое целое имеет шесть степеней свободы. Сложность изучения движений конькобежца заключается в том, что звенья его тела перемещаются в пространстве не только вперед-назад, но и вправо-влево, вверх-вниз, описывая при этом различные траектории. Если у какого-либо тела закрепляется одна точка, то оно теряет три степени свободы, т. е. оно не может двигаться вдоль трех осей координат, а будет иметь возможность только вращаться вокруг этих осей. Поэтому, например, бедро конькобежца относительно туловища может только вращаться вокруг трех осей тазобедренного сустава (сгибание-разгибание, супинация-пронация, отведение-приведение).

Костная система двигательного аппарата конькобежца соединена между собой посредством подвижных соединений, называемых суставами. Каждый сустав имеет строго определенную форму и строение, в результате чего количество степеней свободы движения в нем может варьироваться от 1 до 3. Нам важно знать те движения, которые можно осуществ-

лять в каждом суставе при беге на коньках, поэтому остановимся более подробно на их характеристике.

Движение туловища осуществляется в суставах позвоночного столба вокруг трех осей: поперечной (сгибание-разгибание), переднезадней (наклоны вправо-влево) и вертикальной (скручивание или повороты туловища). При беге на коньках основным является сгибание туловища при опускании в посадку. В отдельные моменты возможны небольшие смещения вокруг переднезадней оси, а именно отведение плеч, например, при беге по повороту. Все остальные движения лишние, и спортсмен не должен их выполнять.

Бег с движением верхних конечностей осуществляется за счет движений в плечевом, локтевом и лучезапястном суставах. В целом верхняя конечность обладает 27 степенями подвижности, из которых 20 приходится на пальцы, 2 — на лучезапястный, 2 — на локтевой и 3 — на плечевой суставы. При анализе движений при беге на коньках необходимо рассматривать в основном вращения, осуществляемые в трех последних суставах.

Движения нижних конечностей производятся в тазобедренном, коленном и голеностопном суставах.

Изучение функций суставов позволяет определить, какое движение и с какой амплитудой можно выполнять в каждом суставе, кинематической паре и в целом в кинематической цепи. Это дает тренеру и спортсмену возможность определения целесообразности выполнения тех или иных движений, их последовательности.

Мы уже упоминали о том, что кинематические цепи могут быть незамкнутыми, замкнутыми и замкнувшимися. Примером незамкнутых кинематических цепей у конькобежца могут быть, например, верхние конечности при беге с одной или двумя руками и движения нижних конечностей, когда одна из них находится на опоре, а вторая не касается опоры. В этом случае в каждом соединении возможны изолированные движения. Например, движения правой рукой не влияют на изменение углов в суставах левой руки или движения опорной ноги непосредственно не влияют на движения свободной. В замкнувшихся цепях этого не наблюдается. Если мы соединим руки в «замок» за спиной, то, следовательно, замыкаем кинематическую цепью верхних конечностей и туловища. В этом случае любое движение звеньев одной руки будет вызывать движение звеньев другой. То же наблюдается и в кинематической цепи нижних конечностей, когда обе ноги находятся на опоре. Здесь также любое движение опорной ноги вызывает изменение положения звеньев другой. Взаимообусловленность движений в замкнувшихся цепях необходимо учитывать при анализе техники бега на коньках.

Рис. 2

При биомеханическом анализе движений в каждой кинематической паре указывается амплитуда и направление движения, исходное положение звеньев пары и их взаимное расположение, т. е. угол в суставе, а также положение каждого звена относительно основных плоскостей движения в системе прямоугольных координат. При этом для облегчения анализа все суставы отмечаются точками (центр сустава) и соединяются прямыми линиями. На рис. 2 представлена схема мгновенного положения звеньев тела конькобежцев при движении в сагиттальной плоскости вокруг поперечной оси суставов (сгибание-разгибание). Для примера рассмотрим, какие угловые значения необходимо иметь для характеристики кинематической пары «бедро — голень» опорной ноги: 1 — угол между бедром и голенью; 2 — угол наклона бедра по отношению к горизонтальной плоскости; 3 — угол наклона бедра по отношению к вертикальной плоскости; 4 — угол наклона голени по отношению к горизонтальной плоскости или 5 — угол наклона по отношению к вертикальной плоскости. На рис. 3 представлена схема положения звеньев тела конькобежца во фронтальной плоскости вокруг переднезадней оси в суставах (отведение-приведение).

Кинематические цепи звеньев тела конькобежца представляют собой систему составных

Рис. 3

рычагов, движение в которых осуществляется под действием силы тяги мышц. Но прежде чем перейти к дальнейшему изучению теоретических основ техники бега на коньках, необходимо рассмотреть основные законы механики и понятие силы как физической категории.

II. Основные законы механики и понятие силы. Движение любого тела подчиняется трем основным законам динамики, сформулированным Ньютоном. Первый закон (закон инерции) гласит, что если на тело не действуют другие тела или если их действия взаимно уравновешиваются, то тело сохраняет состояние покоя или равномерного прямолинейного движения. Данное свойство тел называется инерцией. Закон инерции проявляется в том, что если к телу приложена какая-то неуравновешенная сила, то инерция (покоя или движения) тела не позволяет мгновенно изменить его скорость. Это изменение происходит постепенно и тем медленнее, чем больше его масса. Таким образом, нельзя мгновенно изменить скорость движения, а также его направление. С проявлением закона инерции конькобежец встречается постоянно, например при разгоне, падениях.

Второй закон Ньютона гласит, что между силой и изменением скорости (ускорением) существует прямо пропорциональная зависимость, т. е. если сила постоянна по величине и по направлению, то движение тела будет прямолинейным и равноускоренным. В этом случае ускорение а, с которым двигается тело, прямо пропорционально действующей на него силе F, совпадает с ней по направлению и обратно пропорционально массе тела т, т. е.:

F
а = ——— .
т

Отсюда сила, действующая на тело, численно равна произведению массы тела на его ускорение:

F = ma

Сила является векторной величиной, поэтому для ее полной характеристики необходимо обязательно указывать не только численное значение, но и направление в пространстве. Взаимодействие векторных величин в пространстве, т. е. их сложение и вычитание, производится по правилу параллелограмма или треугольника.

Третий закон Ньютона называется законом равенства действия и противодействия, т. е. силы, с которыми взаимодействуют два тела, всегда равны по величине и противоположны по направлению:

F₁ = –F₂

Таким образом, если конькобежец (одно тело) давит при отталкивании на лед (второе те-

ло) с силой 80 кгс, то лед воздействует на конькобежца с такой же силой в 80 кгс. Эта сила называется реакцией опоры.

Бег на коньках возможен только в том случае, когда возникают движущие силы, которые создаются в кинематической системе тела в результате напряжения мышц. Одновременно с движущими силами возникают силы, которые тормозят движение конькобежца. Таким образом создается сложная система взаимоотношения движущих и тормозящих сил, обеспечивающих передвижение конькобежца в пространстве. Ниже мы подробно рассмотрим действие активных тормозящих сил, возникающих при беге на конькобежца.

III. Аэродинамика движений конькобежца. Движение конькобежца осуществляется в газообразной среде, поэтому спортсмен при беге на коньках будет испытывать определенную силу сопротивления этой среды. В общем эта сила зависит от свойств среды (плотности и вязкости воздуха), размеров и формы тела спортсмена, а также от скорости движения конькобежца и выражается следующей формулой:

R_x = SC_x V ².                       (1)

где R_x — сила сопротивления воздушной среды при беге на коньках; S — площадь поперечного сечения тела; С_x — аэродинамический коэффициент; — плотность воздуха; V ² — квадрат скорости движения конькобежца относительно воздушной среды.

Сила сопротивления воздушной среды всегда направлена против движения и является тормозящей силой. Поэтому рассмотрим более подробно зависимость силы сопротивления воздушной среды от каждого из факторов, ее определяющих, с тем чтобы в процессе совершенствования технического мастерства можно было объективно воздействовать на ее уменьшение.

Плотность воздуха. Воздух представляет собой смесь азота (78,09%), кислорода (20,95%), аргона (0,93%), углекислого газа (0,03%), а также других газов и примесей, например водяных паров. Между частицами этих газов действуют молекулярные силы притяжения и отталкивания, которые по мере увеличения расстояния между частицами быстро убывают. Частицы газов имеют определенную массу. Все это обусловливает плотность атмосферного воздуха, которая уменьшается по мере удаления от поверхности земли. Плотность воздуха Q, кг/м³, определяется его массой в единице объема:

m                       
  = ——— .                     (2)
V                        

Плотность воздуха увеличивается с повы-

шением давления и температуры. Плотность воздуха можно вычислить по формуле

P       
  = 0,04737 ——— ,                     (3)
T         

где Р — атмосферное давление, мм. рт. ст.; Т — абсолютная температура воздуха, К.

Например, если атмосферное давление равно 760 мм. рт. ст., а температура воздуха составляет +10°С, то плотность воздуха будет
                                     760
равна: = 0,04737 • ——— +273 = 0,127899,
                                      10°
при этом Т определяется как (t°C+273). Плотность воздуха при –5°С на уровне моря составляет 0,135 кг/м³; на высоте 500 м — 0,130; на высоте 1000 м — 0,119 и на высоте 2000 м — 0,106 кг/м³ (В. Г. Мышкин, 1973).

Масса воздуха своей тяжестью создает атмосферное давление, которое постепенно увеличивается по направлению к поверхности земли и на уровне моря достигает 760 мм. рт. ст. На рис. 4 представлена графическая зависимость изменения атмосферного давления от высоты местности над уровнем моря. Эта зависимость имеет экспоненциальный характер, и давление на любой высоте находится по формуле

         –mgh
        ———
         KT
Р_h = P₀l              (4)

где Р₀ — атмосферное давление на уровне моря (760 мм. рт. ст.); е — основание натуральных логарифмов (2,72); m — масса молекулы; g — ускорение свободного падения; К — постоянная Больцмана; Т — абсолютная температура; h — высота над уровнем моря.

Однако в практической работе определять величину атмосферного давления целесообразно с помощью специальных приборов — барометров.

Поскольку плотность воздуха увеличивается с повышением атмосферного давления, то его снижение будет уменьшать плотность воздуш-

Рис. 4

ной среды, следовательно, и силу сопротивления воздуха движущемуся конькобежцу. Поэтому с увеличением уровня высоты катков по отношению к уровню моря плотность воздуха уменьшается и соответственно снижается сила сопротивления воздушной среды, что (при прочих равных условиях) способствует уменьшению одной из тормозящих сил и, следовательно, повышению скорости бега. М. П. Соколов (1959) указывает, что с повышением катка на 100 м над уровнем моря результаты конькобежцев улучшаются на каждые 500 м дистанции на 0,1 с.

Такое же действие на плотность воздуха оказывает и наличие в нем примесей (в нашем примере — водяных паров). Следовательно, чем меньше в атмосфере водяных паров, тем меньше плотность воздуха и выше спортивные результаты. И, наконец, чем ниже будет температура окружающей среды (воздуха), тем меньше ее плотность, а следовательно, выше скорость бега спортсменов.

Однако положительное действие отмеченных закономерностей на спортивные- результаты находится в определенных границах. Эти условные границы связаны с взаимодействием чисто физических факторов и механики движений конькобежца с биологическими факторами, определяющими работоспособность человеческого организма. Поэтому повышение спортивных результатов возможно только при оптимальном соотношении всех этих факторов. Поясним сказанное на примерах. С точки зрения законов физики чем меньше атмосферное давление, чем суше воздух и чем ниже его температура, тем меньше плотность воздуха и сила его сопротивления конькобежцу. Но для жизнедеятельности организма и спортивной работоспособности такие абсолютные выводы оказываются неприемлемыми. С понижением атмосферного давления уменьшается парциальное давление кислорода, от обеспечения которым в конечной степени зависит работоспособность конькобежца. С понижением температуры окружающей среды ниже определенного комфортного уровня снижается работоспособность мышц. Слишком сухой воздух также оказывает отрицательное влияние на организм спортсмена. Таким образом, только оптимальное воздействие указанных физических факторов (атмосферное давление, влажность, температура) окружающей среды на механику движения и функциональную работоспособность организма конькобежцев позволит добиться высоких спортивных результатов.

Вязкость воздуха. Вязкость есть не что иное, как явление внутреннего трения между его слоями, движущимися с разной скоростью. Рассмотрим, от чего возникает вязкость воздуха, и факторы, влияющие на нее. Для лучшего понимания этого явления условно предположим, что воздух состоит из отдельных па-

Рис. 5

раллельных слоев (рис. 5, А). Известно, что силы взаимного притяжения существуют не только между молекулами воздуха, но и между молекулами воздуха и движущегося в атмосфере тела, с поверхностью которого они соприкасаются. Таким образом, при движении конькобежца в атмосфере к его поверхности «прилипают» частицы воздуха (назовем этот слой воздуха пограничным), т. е. пограничный слой воздуха двигается со скоростью движения конькобежца, в то время как все остальные слои остаются пока относительно неподвижными.

Молекулы газа, переходя из пограничного слоя, движущегося со скоростью бега конькобежца, в соседний слой, ускоряют его движение, а молекулы газа, переходя из неподвижного слоя (или двигающегося с меньшей скоростью), замедляют движение пограничного слоя. В результате получается, что слой воздуха, двигающийся с большей скоростью, как бы увлекает за собой другие слои, двигающиеся с меньшей скоростью или бывшие неподвижными. Согласно третьему закону Ньютона, более медленный слой вызывает при этом торможение более быстрого слоя воздуха, что ведет к выравниванию их скоростей, т. е. к возникновению сил внутреннего трения, характеризующих вязкость воздуха. Таким образом, силы внутреннего трения тормозят движение слоев воздуха относительно друг друга.

На рис. 5, Б стрелками изображены скорости движения воздуха (V) в разных слоях. В непосредственной близости от поверхности тела конькобежца скорость движения воздуха равна скорости бега. По мере удаления от движущегося конькобежца (в перпендикулярном направлении от тела) скорость движения слоев воздуха приближается к нулю. Силы вязкости, действующие между слоями воздуха, располо-

Рис. 6

женными параллельно вектору скорости, увлекают эти слои в движение следом за телом и создают сопротивление его движению.

Величина вязкости воздуха чрезвычайно мала. Так, при температуре 20°С и атмосферном давлении 760 мм рт. ст. вязкость воздуха составляет 1,83 (•10⁶² кгс•с/м²), тогда как воды — 103. Однако в связи с тем, что скорость движения конькобежца, а следовательно, и пограничного слоя воздуха может быть значительной и быстро меняется, то и силы трения получаются здесь значительные, хотя абсолютная вязкость воздуха может быть и малой. Силы вязкости, обусловленные движением слоев воздуха, изменяются прямо пропорционально скорости движения тела конькобежца. Следует учесть, что при встречном ветре силы внутреннего трения слоев воздуха увеличиваются, так как конькобежцу приходится преодолевать инерцию не неподвижно расположенных слоев воздуха, а двигающихся навстречу направлению вектора скорости. При этом разность в скорости движения слоев воздуха друг от друга значительно увеличивается. Вязкость воздуха с повышением температуры увеличивается, так как это увеличивает скорость хаотичного движения молекул и ведет к более частому обмену молекулами между слоями воздуха, т. е. к увеличению сил внутреннего трения.

Таким образом, можно констатировать, что вязкость воздуха зависит от скорости передвижения конькобежца (чем она выше, тем больше вязкость) и от температуры (чем она ниже,

тем меньше вязкость). Кроме того, сила вязкого сопротивления воздуха зависит от объема (или поверхности) тела конькобежца, соприкасающегося с воздухом (чем этот объем меньше, тем лучше; здесь большую выгоду получают конькобежцы с меньшей поверхностью тела); объема слоев воздуха, увлекаемого поверхностью конькобежца (состав ткани верхнего слоя одежды и конфигурации тела), которые зависят от его обтекаемости.

Площадь поперечного сечения. Установлено, что сила сопротивления воздушной среды при беге на коньках прямо пропорциональна площади сечения тела, перпендикулярного направлению движения, т. е. проекции тела на плоскость, перпендикулярную направлению движения (миделево сечение). На рис. 6 представлены площади поперечного сечения тела одного и того же конькобежца в различных положениях и фазах движения.

Площадь поперечного сечения у одного и того же конькобежца зависит от формы и высоты посадки, т. е. от положения туловища относительно линии горизонта (угол наклона вперед), и степени углов сгиба в коленных и голеностопных суставах, а также от положения рук и ног во время движения. Она будет наименьшая в низкой посадке с руками за спиной. Нетрудно заметить, как площадь поперечного сечения тела претерпевает существенные изменения в различных исходных положениях и фазах движения. При беге с движениями одной руки при одной и той же посадке она увеличивается

по сравнению с бегом с руками за спиной, а еще больше она будет при движении обеих рук. При этом движения рук в направлении вперед-назад окажутся более выгодными, чем в поперечном направлении из стороны в сторону. При одинаковых углах в коленных суставах площадь поперечного сечения будет зависеть от угла наклона ног вперед в голеностопных суставах и наклона туловища вперед. В свою очередь при одинаковом наклоне туловища вперед она будет зависеть от наклона вперед в голеностопных суставах и угла сгиба в коленных суставах и т. д. Таким образом, площадь поперечного сечения тела при беге конькобежца не постоянна, а претерпевает определенные изменения в различных фазах движения, поэтому для оптимизации техники бега на коньках и уменьшения тормозящих сил тренер и спортсмен должны учитывать важный фактор — уменьшение площади поперечного сечения, которого можно достигнуть за счет правильной посадки (наклон туловища, углы в коленных и голеностопных суставах), положения головы, рук и ног. Необходимо также отметить, что площадь любого сопротивления при одном и том же исходном положении меняется в зависимости от участка круга (поворот или прямая). При этом следует учитывать, что слишком большой разворот туловища к центру при беге на повороте будет увеличивать площадь поперечного сечения тела конькобежца, так как туловище занимает как бы поперечное положение к направлению движения.

При беге со старта, как правило, туловище выпрямлено и поднято под большим углом к горизонту, что значительно увеличивает площадь поперечного сечения тела. Поэтому и здесь следует одновременно с увеличением скорости бега принимать соответствующее оптимальное положение туловища, т. е. наклонять его вперед.

Определить приблизительную площадь поперечного сечения для отдельных фаз движения можно с помощью следующих методов: сфотографировать конькобежца в определенном положении движения на фоне разбитого на квадраты экрана (например, большого листа бумаги) и на фотографии подсчитать число клеток, заслоненных проекцией частей тела. Зная размеры квадратов и их число, легко определить площадь поперечного сечения. Кроме того, площадь можно определить при помощи планиметра. Сфотографировав конькобежца в фас в нужном исходном положении и зная масштабный коэффициент фотографии, умножением показателей планиметра на данный коэффициент получают площадь поперечного сечения.

В. А. Петров и Ю. А. Гагин (1974) рассчитали, что в среднем площадь поперечного сечения тела конькобежца составляет 0,35 — 0,5 м².

Аэродинамический коэффици-

Рис. 7

ент. Сила сопротивления воздушной среды при беге конькобежца во многом зависит от коэффициента лобового сопротивления тела, называемого аэродинамическим коэффициентом. Величина этого коэффициента зависит от конфигурации посадки конькобежца и состояния его верхней одежды (т. е. обтекаемости), а также от ориентации частей тела по отношению к направлению движения. Рассмотрим подробнее, почему сила сопротивления воздушной среды зависит от обтекаемости тела. Выше мы отмечали, что сила сопротивления прямо пропорциональна площади поперечного сечения тела и чем эта площадь больше, тем больше лобовое сопротивление. Однако сама по себе площадь поперечного сечения тела еще не дает полного ответа на вопрос о возможной силе сопротивления среды. На рис. 7, заимствованном из учебника физики, показаны три тела с одинаковой площадью поперечного сечения, но разной формы. Установлено, что при их движении с одинаковой скоростью сила лобового сопротивления среды тела А (диск) будет в 30 раз больше, а тела Б (шаровидная форма) в 5 раз больше, чем тела В (каплеобразная форма). Основная причина этого явления заключается в их форме (обтекаемости), поскольку все остальные параметры (скорость, плотность воздуха, площадь лобового сопротивления) движения всех трех тел одинаковы.

Чтобы понять причину такого явления, рассмотрим течения слоев воздуха относительно движущегося тела. Траектории движения частиц (условно слоев) воздуха называются линиями тока. Линии тока — это кривые, направление которых в каждой точке совпадает с направлением скорости в этой точке. Когда соседние слои воздуха двигаются относительно какого-либо тела по параллельным траекториям, т. е. линии тока параллельны, то такое их течение называется ламинарным. В этом случае лобовое сопротивление будет в основном зависеть от сопротивления трения (вязкость), а си-

Рис. 8

лы, возникающие в результате разности давлений впереди и позади тела, будут минимальными. Такое течение слоев воздуха возможно только при движении тела идеально обтекаемой формы (рис. 8,А) и в практике оно встречается очень редко. Практически при движении любого тела, в том числе и конькобежца, образуется турбулентный поток воздуха, который характеризуется тем, что позади движущегося тела образуются завихрения, или вихревые потоки. Они порождаются так называемыми поверхностями раздела, образующимися в потоке при обтекании различных тел.

Для уменьшения лобового сопротивления во время бега необходимо принимать такое положение, при котором позади спортсмена будет образовываться меньше завихрений. Идеально обтекаемой в этом случае является каплеобразная форма (например, тело ракеты, крыло самолета и т. д.). Однако конькобежец в силу объективных причин (строения тела, условия бега и т. д.) не может принять каплеобразную или сигарообразную форму тела. Вместе с тем улучшить обтекаемость конькобежца можно. Для этого прежде всего необходимо выполнять бег в низкой посадке. Спина должна быть округлой формы: голова служит как бы продолжением туловища, а не отклоняется в верх-назад. При беге с руками за спиной последние плотно удерживаются вдоль туловища. На рис. 9 схематически показаны различные варианты положения конькобежца во время бега, обеспечивающие разную степень завихрений позади тела, т. е. с разной степенью обтекаемости.

Обтекаемость конькобежца при движении зависит также от верхнего слоя его спортивного костюма, т. е. от структуры поверхности материала. Чем ворсистее поверхность и чем хуже она прилегает к телу, тем при прочих равных условиях хуже обтекаемость и больше коэффициент аэродинамического сопротивления. Специальные исследования в аэродинамической трубе, проводимые норвежскими, шведскими, западногерманскими и швейцарскими фирмами, изготавливающими спортивную одежду для конькобежцев, показали, что только за счет улучшения структуры поверхностного слоя одежды можно существенно уменьшить силу аэродинамического сопротивления.

Не случайно на смену шерстяным свитеру

Рис. 9

Таблица 1

Аэродинамические коэффициенты сопротивления
(по З. Н. Усманову)

и рейтузам пришли плотно облегающие найлоновые комбинезоны.

Аэродинамический коэффициент С_х можно определить по формуле

                                  h²                          
 C_x = 2C —— ,
                 S     

где С — коэффициент, получаемый опытным путем при продуве модели в аэродинамической трубе; h — рост конькобежца, м; S — площадь поперечного сечения, м².

В. А. Петров и Ю. А. Гагин (1974) приводят аэродинамический коэффициент для конькобежцев в посадке, равный 0,55 — 0,65.

Скорость движения. Сила сопротивления воздушной среды прямо пропорциональна квадрату скорости движения конькобежца относительно воздушных слоев. Данный факт, установленный физиками, объясняется тем, что образующееся вихревое движение воздушного потока позади конькобежца создает разрежение воздуха и сильное уменьшение давления в этой области. Следовательно, конькобежец как бы притягивается силами вихря назад, а лобовое сопротивление при этом увеличивается. Чем выше скорость движущегося в воздушной среде тела, тем больше образуется завихрений и тем больше площадь их образования, а следовательно, сильнее уменьшается давление позади тела. Кроме того, конькобежец как бы увлекает (тащит) за собой завихряющийся воздух, и чем его больше, тем выше сила сопротивления среды.

До сих пор мы рассматривали примеры движения конькобежца в неподвижной воздушной среде. Однако очень часто конькобежцу приходится бегать на коньках при наличии ветра, скорость и направление которого могут оказы-

вать существенное влияние на величину тормозящей силы сопротивления среды и скорость. движения конькобежца. Бег на коньках проходит по круговой замкнутой дорожке, поэтому независимо от направления ветра на конькобежца в определенной последовательности действуют пять его основных разновидностей: 1) встречно-лобовой; 2) встречно-угловой; 3) боковой; 4) попутно-угловой; 5) попутный. Естественно, что в зависимости от направления ветра и его скорости меняется сила сопротивления среды. При встречно-лобовом направлении ветра сила сопротивления среды будет максимальной, а при попутном — минимальной. Учитывая вышесказанное, в формулу определения силы сопротивления воздушной среды (1) необходимо вносить поправку (В. Г. Мышкин, 1973). При безветрии для расчетов берется скорость бега конькобежца. При встречно-лобовом ветре относительная скорость движения V_o определяется суммой скорости бега конькобежца V и скорости ветра V_в

V_o = V + V_в.

При попутном ветре относительная скорость движения определяется разностью скорости бега конькобежца и скорости ветра:

V_o= V – V_в .

При встречно-угловом направлении ветра, дующем на конькобежца под углом а, относительная скорость движения определяется по формуле (В. Г. Мышкин, 1973)

где а — угол между направлением ветра и направлением движения конькобежца (рис. 10, А).

Рис. 10

При боковом ветре V₀ определяется как геометрическая сумма скоростей по формуле (рис. 10, Б)

.

При попутно-угловом ветре V_о определяется по формуле (рис. 10, В)

.

Таким образом, рассматривая аэродинамику движений конькобежца в воздушной среде, мы установили, что сила сопротивления воздуха является многофакторной величиной, оказывающей существенное влияние на уменьшение скорости его бега. Основная задача конькобежца заключается в увеличений скорости бега V, поэтому для уменьшения действия тормозящей силы сопротивления воздуха необходимо стремиться уменьшать действие других ее состав-

ляющих компонентов. Снижение силы сопротивления с уменьшением плотности воздуха позволяет конькобежцам показывать более высокие спортивные результаты на катках, расположенных значительно выше уровня моря (полувысокогорные и высокогорные). Уменьшение плотности и вязкости воздуха, в принципе, не зависит от воздействия на них человека. Поэтому объективно уменьшить силу сопротивления воздуха можно только за счет уменьшения площади лобового сопротивления и аэродинамического коэффициента. А воздействие на эти показатели уже находится во власти тренера и спортсмена. Следовательно, в процессе совершенствования технического мастерства необходимо знать и учитывать действие всех вышеописанных закономерностей и в соответствии с этим выбирать пути оптимизации структуры движений конькобежцев с целью улучшения спортивных результатов.

IV. Сила трения поверхности коньков о лед. При движении одного тела по поверхности другого возникает сопротивление движению, называемое трением. Поскольку сила трения оказывает сопротивление движению, то она всегда направлена по касательной к плоскости соприкасаемых поверхностей в противоположную сторону по отношению к движущей силе и, следовательно, является тормозящей силой. Поэтому при беге на коньках спортсмену постоянно приходится преодолевать силу трения, возникающую между поверхностью лезвия коньков и поверхностью льда. Рассмотрим основные закономерности возникновения и действия силы трения и факторы, от которых зависит ее величина.

Различают три вида трения: трение покоя, трение скольжения и трение качения. Мы остановимся более подробно на их характеристике в следующим сборнике.

ТЕХНИЧЕСКАЯ ПОДГОТОВКА

С ЧЕМПИОНАТА МИРА ПО СПРИНТЕРСКОМУ МНОГОБОРЬЮ 1979 г.

В предыдущем номере сборника мы уже говорили о выполнении ряда элементов техники бега зарубежными спортсменами — призерами чемпионата. Основное внимание было сосредоточено на тех элементах, выполнение которых у зарубежных спортсменов было более совершенным, чем у наших.

Наблюдая за бегом во время чемпионата мира в Инцеле в феврале 1979 г., а также просматривая кинофильмы и анализируя имеющиеся кинограммы, можно отметить у зарубежных спортсменов:

а) более низкую посадку, особенно в беге по повороту; последнее частично достиглось за